Riceviamo la nota del prof. Franco Gismondi, docente di Matematica e Fisica del Liceo Ginnasio Luigi Sodo di Cerreto Sannita che, negli attuali tempi di Didattica a Distanza Integrata, vuole rievocare esperimenti effettuati nello scorso anno con i suoi studenti: “Pendoli: una questione di lunghezza”. Hanno partecipato gli studenti del III Liceo Maddalena Contestabile, Raffaele D’Aronzo, Alessandro Di Nallo, Benedetta Izzo Pascale, Pasquale Merola, Katia Parente, Emanuela Petrillo, Maria Romano, Luciana Torrillo, Chiara Velardo.
“Con una funicella appendiamo un qualunque oggetto ed abbiamo fatto il pendolo. Anche senza provare, sappiamo che se lo lasciamo muovere liberamente oscilla con un’ampiezza che dipende dalla spinta iniziale. Se abbiamo voglia di spingerci in qualche dettaglio, possiamo notare che il tempo impiegato per una oscillazione dipende dalla lunghezza della funicella. Più si utilizza una funicella lunga, più tempo impiega il pendolo a compiere una oscillazione. Non è comunque corretto dire che la lunghezza e il tempo sono direttamente proporzionali perché questa espressione ha un significato matematico molto più preciso del semplice aumento contemporaneo di due grandezze.
Un aspetto poco intuitivo riguarda l’ampiezza delle oscillazioni. Può sembrare strano ma il tempo per compiere una oscillazione molto piccola è esattamente lo stesso di quello per una oscillazione un poco più grande. Il fenomeno va sotto il nome di “isocronismo delle piccole oscillazioni”, e fu scoperto dal giovane Galileo osservando le oscillazioni di una lampada che pendeva dal soffitto nel duomo di Pisa. Dalla metà del XVII secolo fino alla fine del secolo scorso questa particolarità è stata sfruttata per la realizzazione di orologi a pendolo di estrema precisione.
Un’altra particolarità, forse ancora meno intuitiva dell’isocronismo, riguarda la massa pendolare: un pendolo pesante ha un periodo di oscillazione più lungo di un pendolo leggero? E ancora: un pendolo di legno ha un periodo diverso da uno di metallo? Ad entrambe le domande la risposta è no. Pendoli di uguale lunghezza hanno lo stesso periodo di oscillazione qualunque sia la loro massa e qualunque sia il materiale di cui sono costituiti. Il periodo di un pendolo cioè dipende solo dalla sua lunghezza ed è dato dalla formula:
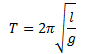
dove abbiamo indicato con T, in secondi, il tempo che il pendolo impiega a compiere una oscillazione completa (sia il tic che il tac) e con l, in metri, la sua lunghezza. π è il noto “pi greco” pari a circa 3.14 e g è l’accelerazione di gravità pari a circa 9.8 m/sec2. Se ad esempio prendiamo in pendolo lungo 25 cm (0.25 m), il suo periodo di oscillazione sarà
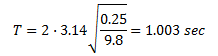
cioè impiega 1 secondo par completare il tic-tac. Se vogliamo un pendolo che impieghi 2 secondi per completare la sua oscillazione, non si deve farlo di lunghezza doppia ma di lunghezza quadrupla (per via della radice quadrata perché 2= ) e basta così con i dettagli matematici.
I ragazzi di III liceo del Luigi Sodo hanno studiato il moto del pendolo in alcuni esperimenti sia qualitativi che quantitativi, realizzati nel laboratorio di fisica della scuola nel mese di settembre 2019.

Sono state appese al soffitto del laboratorio due sottili funicelle di 4 m. Ad una è stato legato un peso di bilancia di 1 Kg ed all’altra è stata legata la scarpa da ginnastica di una alunna, certamente più leggera. Lasciati oscillare contemporaneamente, i due pendoli mantengono il sincronismo perché impiegano lo stesso tempo a compiere una oscillazione. Su molte oscillazioni si nota un leggero ritardo del pendolo più pesante rispetto all’altro. Alla fine dell’esperimento però si è notato che il peso da 1 Kg ha provocato un leggero allungamento della sua funicella perciò il pendolo è risultato di lunghezza maggiore, quindi più lento. Successivamente il pendolo da 1 Kg è stato messo in moto con oscillazioni molto piccole e quello “a scarpa” con oscillazioni più grandi. Anche in questo caso oscillavano con lo stesso periodo confermando “l’isocronismo delle piccole oscillazioni”. Si è proceduto quindi alla verifica sperimentale della formula del periodo T.
Utilizzando il cronometro disponibile in tutti i telefonini è stato misurato il periodo di oscillazione del pendolo da 1 Kg. Poiché i tempi di reazione “umani” si aggirano intorno ai decimi di secondo, la misura effettuata con il cronometro a comando manuale comporta un errore di questo ordine di grandezza. Se si misurano tempi molto lunghi questo errore è trascurabile, non lo è invece se si ha a che fare con tempi brevi. Per migliorare la precisione allora, invece di una sola oscillazione, ne sono state cronometrate 10 consecutive ed il tempo misurato è stato diviso per 10.
Sono state effettuate 6 misure per altrettante lunghezze diverse del pendolo. I risultati ottenuti sono riportati nella tabella seguente: Nella prima colonna la lunghezza del pendolo, nella seconda il tempo misurato con il cronometro e nella terza il tempo calcolato con la formula. Dalla tabella è stato tratto il grafico
| lunghezza pendolo (m) | tempo misurato (sec) | tempo calcolato (sec) |
| 3.93 | 3.83 | 3.9748 |
| 2.84 | 3.38 | 3.3789 |
| 2.00 | 2.64 | 2.8355 |
| 1.45 | 2.47 | 2.4143 |
| 0.72 | 1.70 | 1.7013 |
| 0.39 | 1.30 | 1.2521 |
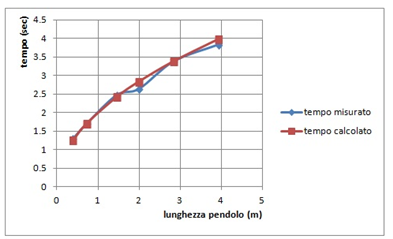
I risultati sperimentali sono abbastanza vicini a quelli teorici, tranne il dato a 2.00 m. Probabilmente in questo punto c’è stata poca attenzione nella misura del tempo o della lunghezza. Complessivamente si può affermare che, entro gli errori sperimentali, la verifica è stata positiva.
Il video dell’esperimento è disponibile sul sito del liceo Luigi Sodo www.liceosodo.com oppure su YouTube al canale “liceosodo”









